Noise Processes¶
The stochastic.processes.noise module provides classes for generating
noise processes.
Gaussian increments
Colored noise
Gaussian increments¶
Noise processes which are increments of their continuous counterparts.
-
class
stochastic.processes.noise.GaussianNoise(t=1, rng=None)[source]¶ Gaussian noise process.
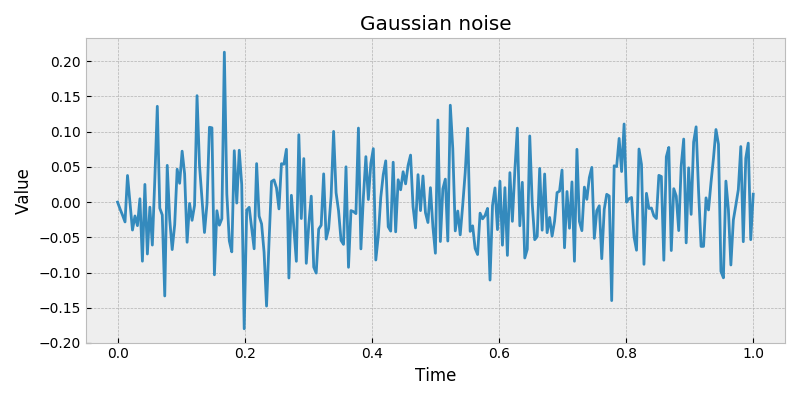
Generate a sequence of Gaussian random variables.
- Parameters
t (float) – the right hand endpoint of the time interval \([0,t]\) for the process
rng (numpy.random.Generator) – a custom random number generator
-
sample(n)[source]¶ Generate a realization of Gaussian noise.
Generate a Gaussian noise realization with n increments.
- Parameters
n (int) – the number of increments to generate.
-
sample_at(times)[source]¶ Generate Gaussian noise increments at specified times from zero.
- Parameters
times – a vector of increasing time values for which to generate noise increments.
-
property
t¶ End time of the process.
-
times(n)¶ Generate times associated with n increments on [0, t].
- Parameters
n (int) – the number of increments
-
class
stochastic.processes.noise.FractionalGaussianNoise(hurst=0.5, t=1, rng=None)[source]¶ Fractional Gaussian noise process.
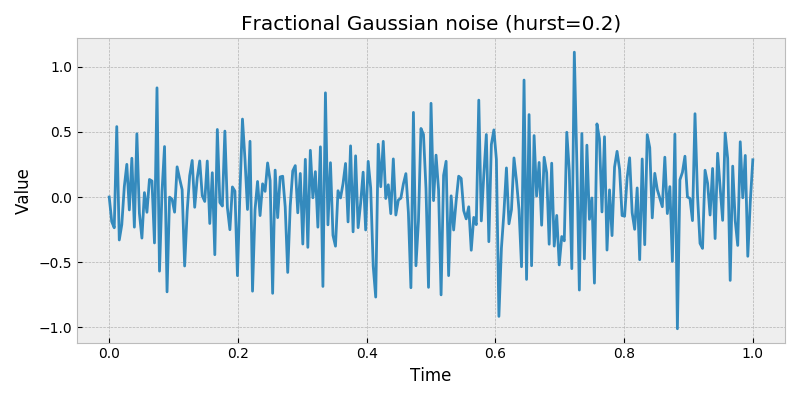
Generate sequences of fractional Gaussian noise.
Hosking’s method:
Hosking, Jonathan RM. “Modeling persistence in hydrological time series using fractional differencing.” Water resources research 20, no. 12 (1984): 1898-1908.
Davies Harte method:
Davies, Robert B., and D. S. Harte. “Tests for Hurst effect.” Biometrika 74, no. 1 (1987): 95-101.
- Parameters
hurst (float) – The Hurst parameter value in \((0,1)\).
t (float) – the right hand endpoint of the time interval \([0,t]\) for the process
rng (numpy.random.Generator) – a custom random number generator
-
property
hurst¶ Hurst parameter.
-
sample(n, algorithm='daviesharte')[source]¶ Generate a realization of fractional Gaussian noise.
- Parameters
n (int) – number of increments to generate
algorithm (str) – either ‘daviesharte’ or ‘hosking’ algorithms
-
property
t¶ End time of the process.
-
times(n)¶ Generate times associated with n increments on [0, t].
- Parameters
n (int) – the number of increments
Colored noise¶
Signals with spectral densities proportional to the power law.
-
class
stochastic.processes.noise.BlueNoise(t=1, rng=None)[source]¶ Blue noise.
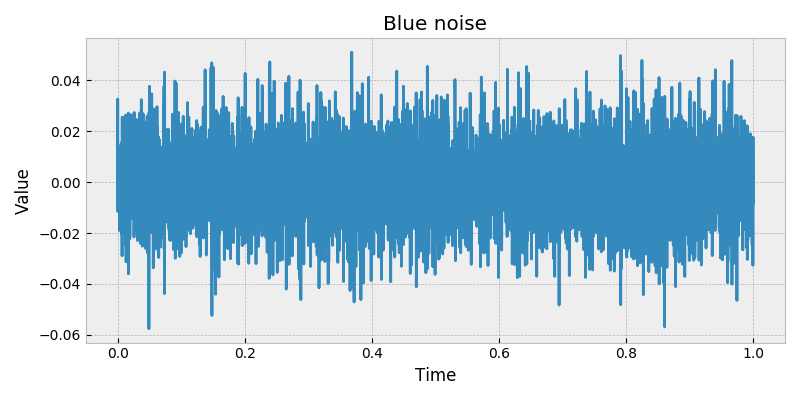
Colored noise, or power law noise with spectral density exponent \(\beta = -1\).
- Parameters
t (float) – the right hand endpoint of the time interval \([0,t]\) for the process
rng (numpy.random.Generator) – a custom random number generator
-
sample(n)¶ Generate a realization of colored noise.
Generate a colored noise realization with n increments.
- Parameters
n (int) – the number of increments to generate.
-
property
t¶ End time of the process.
-
times(n)¶ Generate times associated with n increments on [0, t].
- Parameters
n (int) – the number of increments
-
class
stochastic.processes.noise.BrownianNoise(t=1, rng=None)[source]¶ Brownian (red) noise.
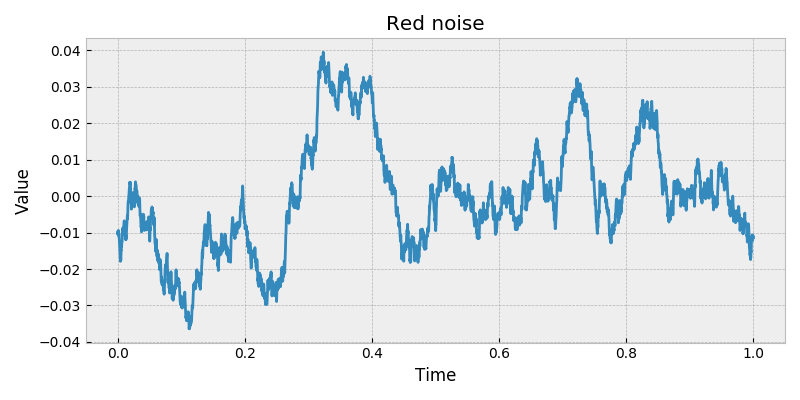
Colored noise, or power law noise with spectral density exponent \(\beta = 2\).
- Parameters
t (float) – the right hand endpoint of the time interval \([0,t]\) for the process
rng (numpy.random.Generator) – a custom random number generator
-
sample(n)¶ Generate a realization of colored noise.
Generate a colored noise realization with n increments.
- Parameters
n (int) – the number of increments to generate.
-
property
t¶ End time of the process.
-
times(n)¶ Generate times associated with n increments on [0, t].
- Parameters
n (int) – the number of increments
-
class
stochastic.processes.noise.ColoredNoise(beta=0, t=1, rng=None)[source]¶ Colored noise processes.
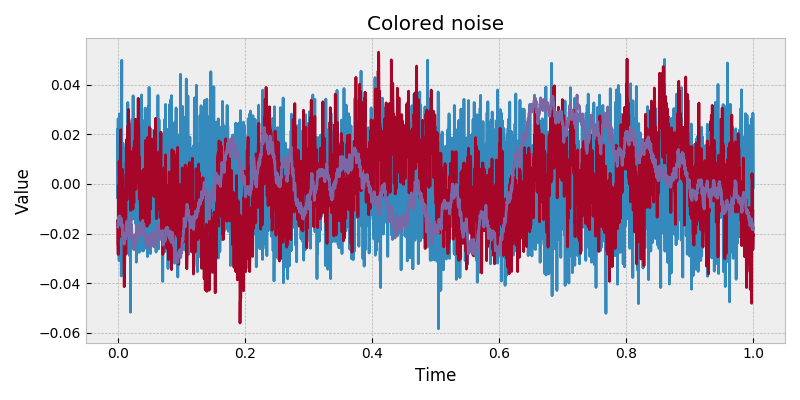
Also referred to as power law noise, colored noise refers to noise processes with power law spectral density. That is, their spectral density per unit bandwidth is proportional to \((1/f)^\beta\), where \(f\) is frequency with exponent \(\beta\).
Uses the algorithm from:
Timmer, J., and M. Koenig. “On generating power law noise.” Astronomy and Astrophysics 300 (1995): 707.
Generates a normalized power-law spectral noise.
- Parameters
beta (float) – the power law exponent for the spectral density, with 0 being white noise, 1 being pink noise, 2 being red noise (Brownian noise), -1 being blue noise, -2 being violet noise. Default is 0 (white noise).
t (float) – the right hand endpoint of the time interval \([0,t]\) for the process
rng (numpy.random.Generator) – a custom random number generator
-
property
beta¶ Power law exponent.
-
sample(n)[source]¶ Generate a realization of colored noise.
Generate a colored noise realization with n increments.
- Parameters
n (int) – the number of increments to generate.
-
property
t¶ End time of the process.
-
times(n)¶ Generate times associated with n increments on [0, t].
- Parameters
n (int) – the number of increments
-
class
stochastic.processes.noise.RedNoise(t=1, rng=None)[source]¶ Red (Brownian) noise.

Colored noise, or power law noise with spectral density exponent \(\beta = 2\).
- Parameters
t (float) – the right hand endpoint of the time interval \([0,t]\) for the process
rng (numpy.random.Generator) – a custom random number generator
-
sample(n)¶ Generate a realization of colored noise.
Generate a colored noise realization with n increments.
- Parameters
n (int) – the number of increments to generate.
-
property
t¶ End time of the process.
-
times(n)¶ Generate times associated with n increments on [0, t].
- Parameters
n (int) – the number of increments
-
class
stochastic.processes.noise.PinkNoise(t=1, rng=None)[source]¶ Pink (flicker) noise.
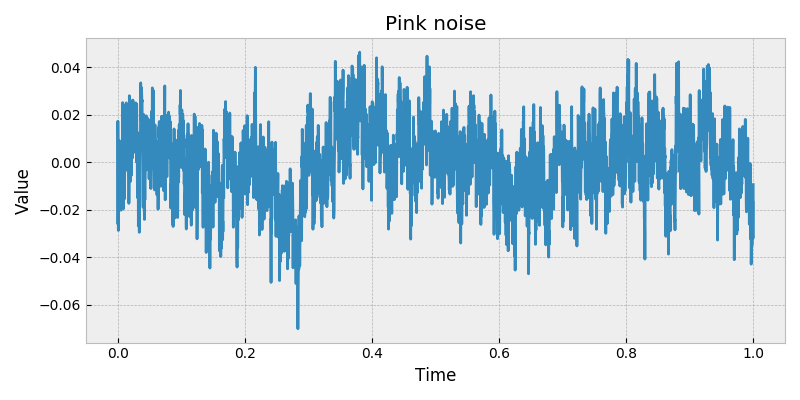
Colored noise, or power law noise with spectral density exponent \(\beta = 1\).
- Parameters
t (float) – the right hand endpoint of the time interval \([0,t]\) for the process
rng (numpy.random.Generator) – a custom random number generator
-
sample(n)¶ Generate a realization of colored noise.
Generate a colored noise realization with n increments.
- Parameters
n (int) – the number of increments to generate.
-
property
t¶ End time of the process.
-
times(n)¶ Generate times associated with n increments on [0, t].
- Parameters
n (int) – the number of increments
-
class
stochastic.processes.noise.VioletNoise(t=1, rng=None)[source]¶ Violet noise.
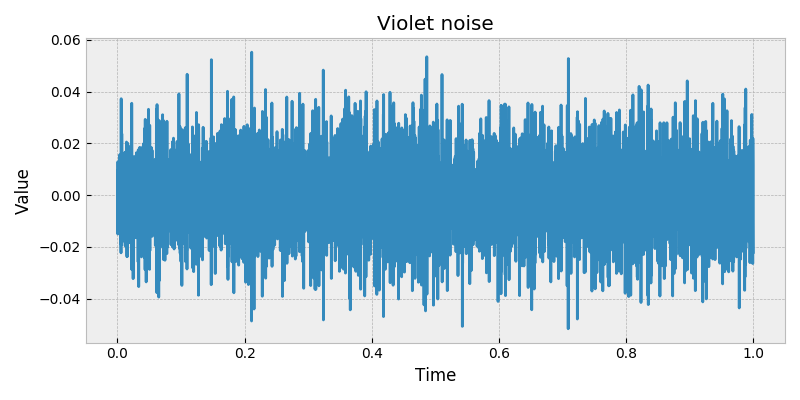
Colored noise, or power law noise with spectral density exponent \(\beta = -2\).
- Parameters
t (float) – the right hand endpoint of the time interval \([0,t]\) for the process
rng (numpy.random.Generator) – a custom random number generator
-
sample(n)¶ Generate a realization of colored noise.
Generate a colored noise realization with n increments.
- Parameters
n (int) – the number of increments to generate.
-
property
t¶ End time of the process.
-
times(n)¶ Generate times associated with n increments on [0, t].
- Parameters
n (int) – the number of increments
-
class
stochastic.processes.noise.WhiteNoise(t=1, rng=None)[source]¶ White noise.
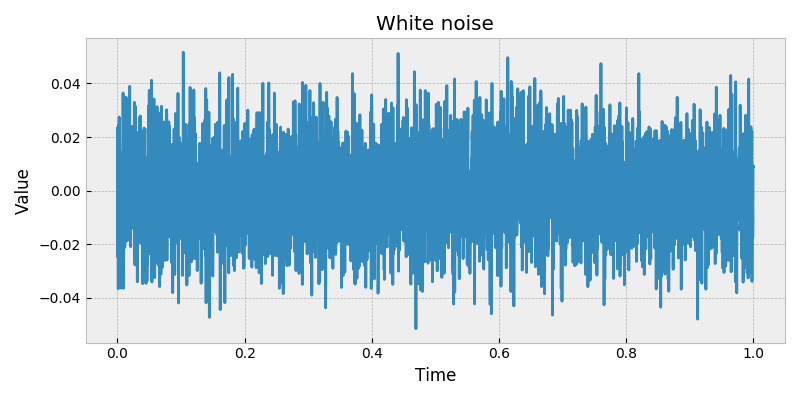
Colored noise, or power law noise with spectral density exponent \(\beta = 0\).
- Parameters
t (float) – the right hand endpoint of the time interval \([0,t]\) for the process
rng (numpy.random.Generator) – a custom random number generator
-
sample(n)¶ Generate a realization of colored noise.
Generate a colored noise realization with n increments.
- Parameters
n (int) – the number of increments to generate.
-
property
t¶ End time of the process.
-
times(n)¶ Generate times associated with n increments on [0, t].
- Parameters
n (int) – the number of increments